Spoiler Warning: By the end of this first post, I still haven’t actually handled any collisions.
This post isn’t going to be as straight forward as my previous posts. I’ve rewritten this a few times, and decided just a consciousness dump might be good for me, and good for others to understand that things aren’t always clear or easy. I might want to have a different tag for stream of consciousness posts like this.
I’m going to start turning this whole project into a bunch of teeny programs to prove concepts. My project is getting cluttered with junk and it doesn’t even really do anything, yet. The good news is that there’s going to be a git repository that sort of grows and changes as the project goes on, and maybe turns into a tool someone can use to learn from, or at very least, something for me to look back on and be like “what was I thinking?”
As I said in a previous post, I’m trying to implement as much as I can without using the Playdate SDK. If you’re here to learn how to use the Playdate’s built in colliders, head over to the official SDK. The link changes often so your best bet is to just go to https://play.date/dev/ and seach “Sprite collision detection”, and while you’re at it, you can look at the library they based their collision detection on. https://github.com/kikito/bump.lua . The SDK is wonderful, I’m here’s to learn how to do as much of this as I can myself.
Now that we got that out of the way, let’s see how bad I am at implementing this myself. I’ve read a bulk of the bump library, and I’ve cried when reading Game Engine Architecture by Jason Gregory so I can probably do this. I also read the entire source code for Celeste on the Pico8.
My original version of this game, the engine handled all this for me, so I’m feeling a little overwhelmed at having such a blank slate, freedom is scary.
The Plan
This game doesn’t require anything too fancy, so I’m going to start out with two types of collisions.
Tilemap
AABB (Axis-Aligned Bounding Box)
That’s it.
Tilemap
Tilemap is going to work like this. The screen / level will be split into a grid of 8×8 pixels. Each tile will have a flag associated. These flags will be “solid”, “not-solid” to start out. I’ll likely add different things to have “disappears when player touches it”, and one way platforms, special static blocks and things like that, but we’ll burn that bridge when we get there.
The benefit of a tilemap is having to do less collision checks.
TILEMAP IMAGE
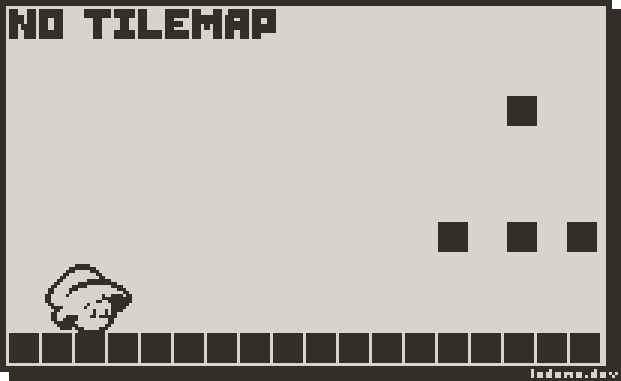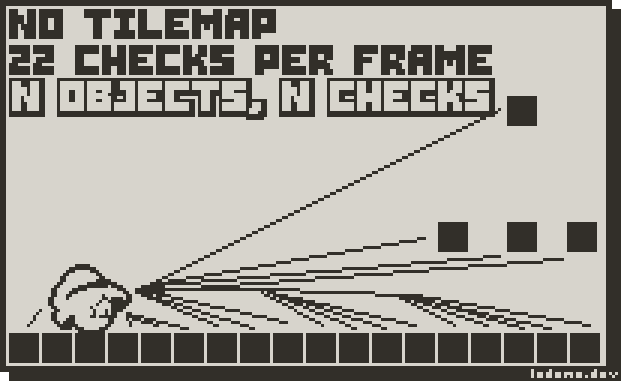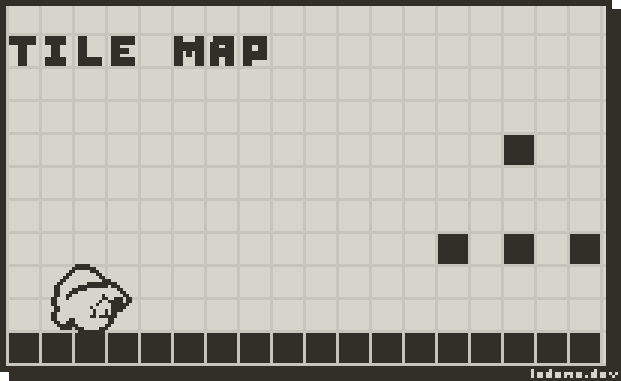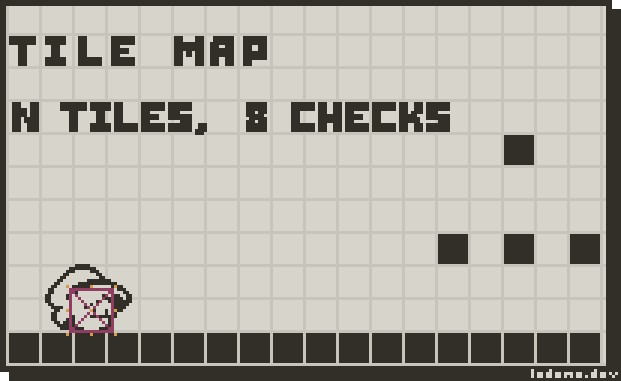
Pros: It doesn’t matter if there’s a million tiles, or 1 tile, the amount of collision checks is constant. Now, that image is a little misleading, you only need to check for collisions in the direction you’re moving, and might need to check for more than 1 collision in a specific direction if the object is bigger than a tile. That being said, it’s still better than checking against every single possible thing in a scene.
Cons: Objects can’t move (less than the size of a tile).
Now take a minute, think about how you would implement this. If you haven’t read the post on bit, bytes and data types https://blog.lodomo.dev/2025/04/20/cs-bits-bytes-and-data-types-in-lua/ check it out. There’s loads of ways we can abstract the map.
What if each tile just had a number? that gives us 4,294,967,296 options for each tile. If we could store it in chars, that would be nice, but iterating through strings in Lua isn’t very efficient. Let’s check out some tests.
Let’s do a little test on a single screen.
X_BOOL_50x30 = {}
for i = 1, 30 do
X_BOOL_50x30[i] = {}
for j = 1, 50 do
X_BOOL_50x30[i][j] = false
end
end
X_NUM_50x30 = {}
for i = 1, 30 do
X_NUM_50x30[i] = {}
for j = 1, 50 do
X_NUM_50x30[i][j] = 0
end
end
X_STRING_50x30 = {}
for i = 1, 30 do
X_STRING_50x30[i] = "00000000000000000000000000000000000000000000000000"
end

So now there’s 50 tiles * 30 tiles * 30 tables (one for each row) for the bool and num tables. That takes a whopping 33,712 bytes of memory for a single screen, just for flag data.
The table of strings is just 30 items, 30 strings each one 50 chars long. It’s less than 1/10th of the size of the number/boolean tables and still has 255 possible tile options per tile.
Let’s test how well lua can go through all these and see if that overhead is worth it or not.
I loop through and get the value of every data member, and do nothing with it, this is purely just a table lookup. Then it prints to the screen what the average time for 1500 (50×30) lookups.

Ooof. Welp, I’m a little concerned. For strings, that’s still a very very small amount of time per look up (0.0085~ ms) but it’s still about 4x slower than numbers.
“The real problem is that programmers have spent far too much time worrying about efficiency in the wrong places and at the wrong times; premature optimization is the root of all evil (or at least most of it) in programming.” – Donald Knuth
Look, Don, I just don’t want this slowing me down later that my tile maps are causing problems.
I have 16,000,000 bytes to play with in RAM, a full screen tilemap is 33,000? maybe it’s worth the overhead to have faster lookups, and just be better about loading on the fly. The time to render each frame is around 20-30 milliseconds, and that is a much more precious resource.
Now onto the collisions…
The Code
So I think in a final version the logic will be a bit different to keep objects to a more defined job they handle, but this will be something that works. Make it exist, then make it good.
Creates a tile map that has colliders 1 tile in from the edge, all the way around.
for row = 1, ROWS do
TILE_MAP[row] = {}
for col = 1, COLS do
if row == 2 or row == ROWS - 1 or col == 2 or col == COLS - 1 then
TILE_MAP[row][col] = 1
else
TILE_MAP[row][col] = 0
end
end
end
Color in those tiles
for row = 1, #TILE_MAP do
for col = 1, #TILE_MAP[row] do
local tile = TILE_MAP[row][col]
if tile == 1 then
gfx.fillRect((col - 1) * CELL, (row - 1) * CELL, CELL, CELL)
end
end
end
Now we need a moving object.
PLAYER = {
x = 120,
y = 120,
width = 16,
height = 16,
velocity = {
x = 1,
y = 1,
},
draw = function(self)
gfx.fillRect(self.x, self.y, self.width, self.height) -- x, y, width, height
end,
update = function(self)
self.x = self.x + self.velocity.x
self.y = self.y + self.velocity.y
end,
}
Right now there is no tile checking, but I wanted to make sure this works. Test at every step.

drawVelocity = function(self)
local l_x = self.x
local l_y = self.y
local r_x = self.x + self.width
local r_y = self.y + self.height
gfx.drawLine(l_x, l_y, l_x + self.velocity.x, l_y + self.velocity.y)
gfx.drawLine(r_x, l_y, r_x + self.velocity.x, l_y + self.velocity.y)
gfx.drawLine(l_x, r_y, l_x + self.velocity.x, r_y + self.velocity.y)
gfx.drawLine(r_x, r_y, r_x + self.velocity.x, r_y + self.velocity.y)
end,

Ok, so now these lines will be where the next frame will be. I made the speed 4 pixels per frame, going at a 45 degree angle down and right.
Since we have the line of the direction were going it helps me visualize what I need to do, and then start to process that into logic. In psuedo code:
If the velocity in the x direction is positive:
check along the right side of the new position
If the velocity in the x direction is negative:
check along the left side of the new position
If the velocity is the x direction is neutral:
there cannot be new x-direction collision, do nothing.
If the velocity in the y direction is positive:
check along the bottom of the new position
If the velocity in the y direction is negative:
check along the top of the new position
If the velocity in the y direction is neutral:
there cannot be new y-direction collision, do nothing.
AAAND this is where I think I’m going to end it this week. I’d rather give you all little updates as I finish them than nothing. Keeps me honest to keep working.
Until Next Time,
Lodomo

Leave a Reply